Trisha Shetty (Editor)

Cramér's conjecture

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Cramér's conjecture

In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936, is an estimate for the size of gaps between consecutive prime numbers: intuitively, that gaps between consecutive primes are always small, and the conjecture quantifies asymptotically just how small they must be. It states that

Contents

p n + 1 − p n = O ( ( log ⁡ p n ) 2 ) ,  

where pn denotes the nth prime number, O is big O notation, and "log" is the natural logarithm. While this is the statement explicitly conjectured by Cramér, his argument actually supports the stronger statement

lim sup n → ∞ p n + 1 − p n ( log ⁡ p n ) 2 = 1 ,

and this formulation is often called Cramér's conjecture in the literature. However, this stronger formulation is not supported by more accurate heuristic models, which nevertheless support the first version of Cramér's conjecture.

Neither form of Cramér's conjecture has yet been proven or disproven.

Conditional proven results on prime gaps

Cramér gave a conditional proof of the much weaker statement that

p n + 1 − p n = O ( p n log ⁡ p n )

on the assumption of the Riemann hypothesis. The best known unconditional bound is

p n + 1 − p n = O ( p n 0.525 )

due to Baker, Harman, and Pintze.

In the other direction, E. Westzynthius proved in 1931 that prime gaps grow more than logarithmically. That is,

lim sup n → ∞ p n + 1 − p n log ⁡ p n = ∞ .

His result was improved by R. A. Rankin, who proved that

lim sup n → ∞ p n + 1 − p n log ⁡ p n log ⁡ log ⁡ p n log − 2 ⁡ log ⁡ log ⁡ p n log ⁡ log ⁡ log ⁡ log ⁡ p n > 0.

Paul Erdős conjectured that the left-hand side of the above formula is equal to infinity, and this was proven in 2014 by Kevin Ford, Ben Green, Sergei Konyagin, and Terence Tao.

Heuristic justification

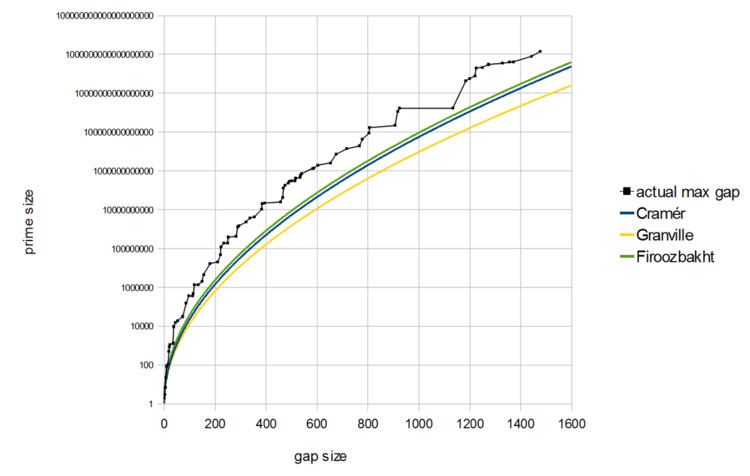
Cramér's conjecture is based on a probabilistic model (essentially a heuristic) of the primes, in which one assumes that the probability of a natural number of size x being prime is 1/log x. This is known as the Cramér model of the primes.

In the Cramér random model,

lim sup n → ∞ p n + 1 − p n log 2 ⁡ p n = 1

with probability one. However, as pointed out by Andrew Granville, Maier's theorem shows that the Cramér random model does not adequately describe the distribution of primes on short intervals, and a refinement of Cramér's model taking into account divisibility by small primes suggests that c ≥ 2 e − γ ≈ 1.1229 … ( A125313), where γ is the Euler–Mascheroni constant. János Pintz has suggested that the limit sup may be infinite, and similarly Leonard Adleman and Kevin McCurley write

As a result of the work of H. Maier on gaps between consecutive primes, the exact formulation of Cramér's conjecture has been called into question [...] It is still probably true that for every constant c > 2 , there is a constant d > 0 such that there is a prime between x and x + d ( log ⁡ x ) c .

Daniel Shanks conjectured the following asymptotic equality for record gaps: G ( x ) ∼ log 2 ⁡ x . This is a stronger statement than Cramér's conjecture.

In the paper J.H. Cadwell has proposed the formula for the maximal gaps: G ( x ) ∼ log ⁡ x ( log ⁡ x − log ⁡ log ⁡ x ) , which for large x implies both the Cramér and Shanks conjectures.

Thomas Nicely has calculated many large prime gaps. He measures the quality of fit to Cramér's conjecture by measuring the ratio

R = log ⁡ p n p n + 1 − p n .

He writes, “For the largest known maximal gaps, R has remained near 1.13.” However, 1 / R 2 is still less than 1, and it does not provide support to Granville's refinement that c should be greater than 1.

References

Cramér's conjecture Wikipedia
(Text) CC BY-SA