 | ||
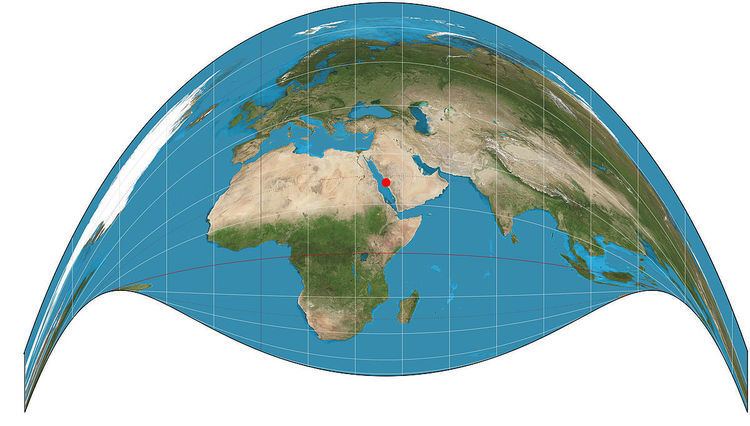
The Craig retroazimuthal map projection was created by James Ireland Craig in 1909. It is a modified cylindrical projection. As a retroazimuthal projection, it preserves directions from everywhere to one location of interest that is configured during construction of the projection. The projection is sometimes known as the Mecca projection because Craig, who had worked in Egypt as a cartographer, created it to help Muslims find their qibla. In such maps, Mecca is the configurable location of interest.
Given latitude φ to plot, latitude φ0 of the fixed location of interest, longitude λ to plot, and the longitude λ0 of the fixed location of interest, the projection is defined by:
But when λ − λ0 = 0, y above is undefined, so instead use the ratio's continuous completion:
