Coupon collector's problem

Understanding the problem

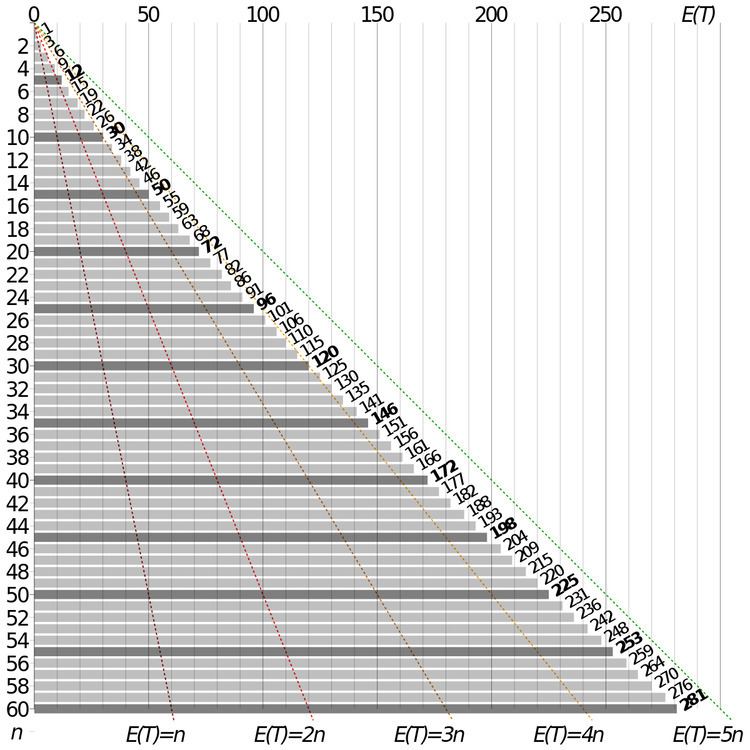
The key to solving the problem is understanding that it takes very little time to collect the first few coupons. On the other hand, it takes a long time to collect the last few coupons. In fact, for 50 coupons, it takes on average 50 trials to collect the very last coupon after the other 49 coupons have been collected. This is why the expected time to collect all coupons is much longer than 50. The idea now is to split the total time into 50 intervals where the expected time can be calculated.

Answer

The following table gives the expected number of tries to get sets of 1 to 100 coupons.

Calculating the expectation

Let T be the time to collect all n coupons, and let t_i be the time to collect the i-th coupon after i − 1 coupons have been collected. Think of T and t_i as random variables. Observe that the probability of collecting a new coupon is p_i = (n − (i − 1))/n. Therefore, t_i has geometric distribution with expectation 1/p_i. By the linearity of expectations we have:

E ⁡ ( T ) = E ⁡ ( t 1 ) + E ⁡ ( t 2 ) + ⋯ + E ⁡ ( t n ) = 1 p 1 + 1 p 2 + ⋯ + 1 p n = n n + n n − 1 + ⋯ + n 1 = n ⋅ ( 1 1 + 1 2 + ⋯ + 1 n ) = n ⋅ H n .

Here H_n is the n-th harmonic number. Using the asymptotics of the harmonic numbers, we obtain:

E ⁡ ( T ) = n ⋅ H n = n log ⁡ n + γ n + 1 2 + o ( 1 ) ,   as   n → ∞ ,

where γ ≈ 0.5772156649 is the Euler–Mascheroni constant.

Now one can use the Markov inequality to bound the desired probability:

P ⁡ ( T ≥ c n H n ) ≤ 1 c .

Calculating the variance

Using the independence of random variables t_i, we obtain:

Var ⁡ ( T ) = Var ⁡ ( t 1 ) + Var ⁡ ( t 2 ) + ⋯ + Var ⁡ ( t n ) = 1 − p 1 p 1 2 + 1 − p 2 p 2 2 + ⋯ + 1 − p n p n 2 < ( n 2 n 2 + n 2 ( n − 1 ) 2 + ⋯ + n 2 1 2 ) < n 2 ⋅ ( 1 1 2 + 1 2 2 + ⋯ + 1 n 2 ) < π 2 6 n 2 .

The π 2 / 6 is a value of the Riemann zeta function (see Basel problem).

Now one can use the Chebyshev inequality to bound the desired probability:

P ⁡ ( | T − n H n | ≥ c n ) ≤ π 2 6 c 2 .

Tail estimates

A different upper bound can be derived from the following observation. Let Z i r denote the event that the i -th coupon was not picked in the first r trials. Then:

P [ Z i r ] = ( 1 − 1 n ) r ≤ e − r / n

Thus, for r = β n log ⁡ n , we have P [ Z i r ] ≤ e ( − β n log ⁡ n ) / n = n − β .

P [ T > β n log ⁡ n ] = P [ ⋃ i Z i β n log ⁡ n ] ≤ n ⋅ P [ Z 1 β n log ⁡ n ] ≤ n − β + 1

Extensions and generalizations

Paul Erdős and Alfréd Rényi proved the limit theorem for the distribution of T. This result is a further extension of previous bounds.

Donald J. Newman and Lawrence Shepp found a generalization of the coupon collector's problem when m copies of each coupon needs to be collected. Let T_m be the first time m copies of each coupon are collected. They showed that the expectation in this case satisfies:

Here m is fixed. When m = 1 we get the earlier formula for the expectation.

Common generalization, also due to Erdős and Rényi:

Wolfgang Stadje has solved the case where the stickers are bought in packets, which contain no duplicates. The results show that for practical applications, say packets of five stickers, the effect of packets is negligible.

Sylvain Vardy and Yvan Velenik derived an optimized strategy including swapping and purchasing missing stickers by Monte Carlo simulation.

In the general case of a nonuniform probability distribution, according to Philippe Flajolet,

Sinai and Olejarz et al calculate a simple approximate bound, as well as exact results, for when coupons are collected in batches (albums) with each batch containing each coupon with probability p and the entire collection may be lost at each step with probability δ. This result has applications to several biological problems.