Conchoid of de Sluze

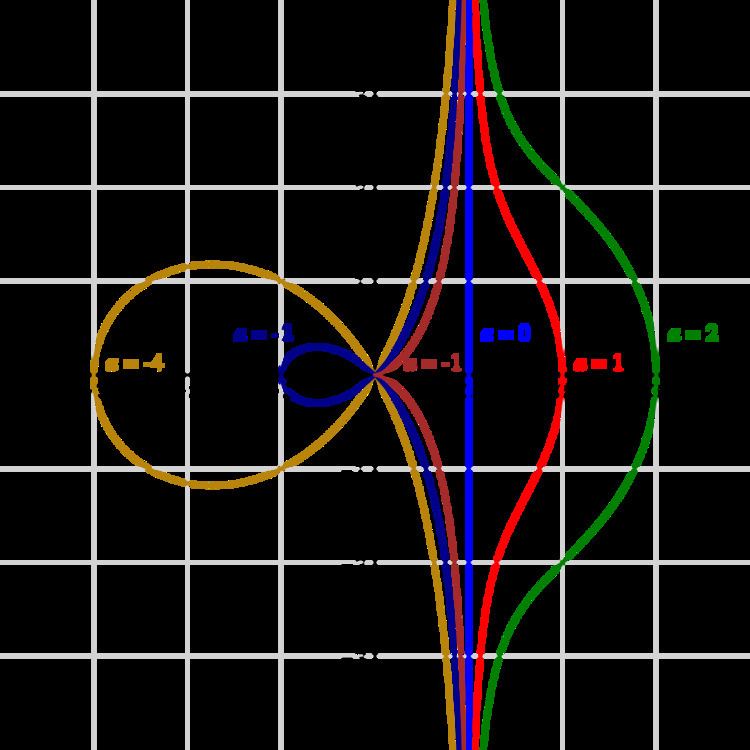
The conchoid(s) of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.

The curves are defined by the polar equation

r = sec ⁡ θ + a cos ⁡ θ .

In cartesian coordinates, the curves satisfy the implicit equation

( x − 1 ) ( x 2 + y 2 ) = a x 2

except that for a=0 the implicit form has an acnode (0,0) not present in polar form.

They are rational, circular, cubic plane curves.

These expressions have an asymptote x=1 (for a≠0). The point most distant from the asymptote is (1+a,0). (0,0) is a crunode for a<−1.

The area between the curve and the asymptote is, for a ≥ − 1 ,

| a | ( 1 + a / 4 ) π

while for a < − 1 , the area is

( 1 − a 2 ) − ( a + 1 ) − a ( 2 + a 2 ) arcsin ⁡ 1 − a .

If a < − 1 , the curve will have a loop. The area of the loop is

( 2 + a 2 ) a arccos ⁡ 1 − a + ( 1 − a 2 ) − ( a + 1 ) .

Four of the family have names of their own:

a=0, line (asymptote to the rest of the family) a=−1, cissoid of Diocles a=−2, right strophoid a=−4, trisectrix of Maclaurin