Circular coloring - Alchetron, The Free Social Encyclopedia

Vertices n Chromatic number ⌈n/k⌉		Edges n(n-2k+1) / 2

Girth { ∞ n = 2 k n n = 2 k + 1 4 2 k + 2 ≤ n < 3 k 3 otherwise {\displaystyle \left\{{\begin{array}{ll}\infty &n=2k\\n&n=2k+1\\4&2k+2\leq n<3k\\3&{\text{otherwise}}\end{array}}\right.} Properties (n − 2k + 1)-regularVertex-transitiveCirculantHamiltonian Notation K n / k {\displaystyle K_{n/k}}

In graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph G , denoted χ c ( G ) can be given by any of the following definitions, all of which are equivalent (for finite graphs).

χ c ( G ) is the infimum over all real numbers r so that there exists a map from V ( G ) to a circle of circumference 1 with the property that any two adjacent vertices map to points at distance ≥ 1 r along this circle.
χ c ( G ) is the infimum over all rational numbers n k so that there exists a map from V ( G ) to the cyclic group Z / n Z with the property that adjacent vertices map to elements at distance ≥ k apart.
In an oriented graph, declare the imbalance of a cycle C to be | E ( C ) | divided by the minimum of the number of edges directed clockwise and the number of edges directed counterclockwise. Define the imbalance of the oriented graph to be the maximum imbalance of a cycle. Now, χ c ( G ) is the minimum imbalance of an orientation of G .

It is relatively easy to see that χ c ( G ) ≤ χ ( G ) (especially using 1. or 2.), but in fact ⌈ χ c ( G ) ⌉ = χ ( G ) . It is in this sense that we view circular chromatic number as a refinement of the usual chromatic number.

Circular coloring was originally defined by Vince (1988), who called it "star coloring".

Coloring is dual to the subject of nowhere-zero flows and indeed, circular coloring has a natural dual notion: circular flows.

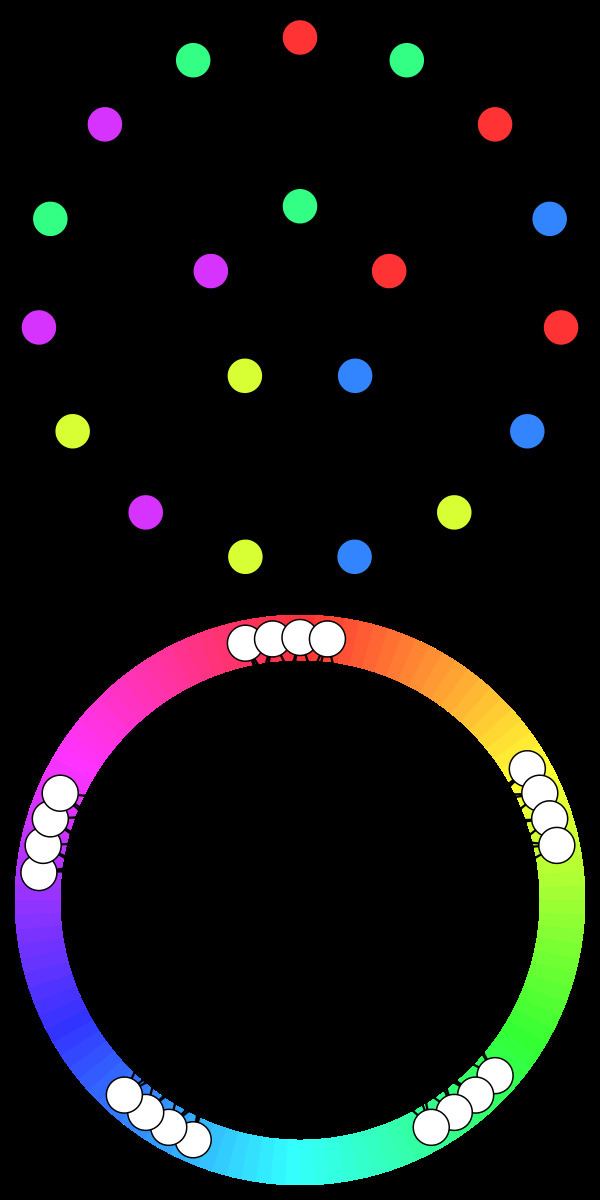
Circular complete graphs

For integers n , k such that n ≥ 2 k , the circular complete graph K_n/k (also known as a circular clique) is the graph with vertex set Z / n Z and edges between elements at distance ≥ k apart. That is, the vertices are numbers {0, 1, ..., n-1} and vertex i is adjacent to:

i+k, i+k+1, ..., i+n-k mod n.

For example, K_n/1 is just the complete graph K_n, while K_{2n+1 / n} is isomorphic to the cycle graph C_2n+1.

A circular coloring is then, according to the second definition above, a homomorphism into a circular complete graph. The crucial fact about these graphs is that K_a/b admits a homomorphism into K_c/d if and only if a/b ≤ c/d. This justifies the notation, since if the rational numbers a/b and c/d are equal, then K_a/b and K_c/d are homomorphically equivalent. Moreover, the homomorphism order among them refines the order given by complete graphs into a dense order, corresponding to rational numbers ≥ 2 . For example

K_2/1 → K_5/2 → K_7/3 → ... → K_3/1 → K_4/1 → ...

or equivalently

K₂ → C₅ → C₇ → ... → K₃ → K₄ → ...

The example on the figure can be interpreted as a homomorphism from the flower snark J₅ into K_5/2 ≈ C₅, which comes earlier than K₃, corresponding to the fact that χ c ( J 5 ) ≤ 2.5 < 3 .

References

Circular coloring Wikipedia

(Text) CC BY-SA