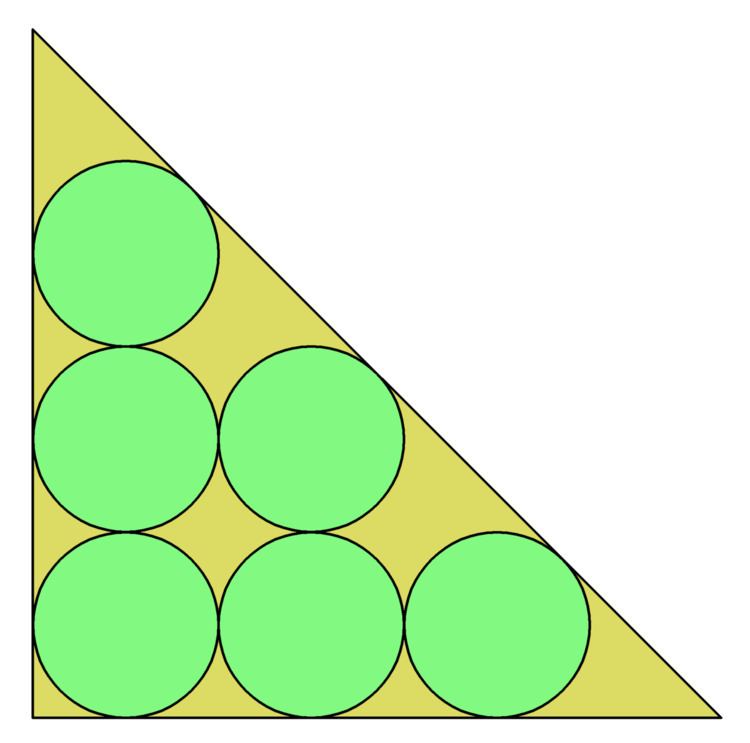
Circle packing in an isosceles right triangle

Circle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right triangle.

Minimum solutions (lengths shown are length of leg) are shown in the table below. Solutions to the equivalent problem of maximizing the minimum distance between n points in an isosceles right triangle, are known to be optimal for n< 8. In 2011 a heuristic algorithm found 18 improvements on previously known optima, the smallest of which was for n=13.