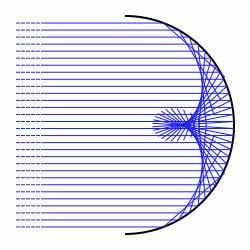
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the concept of caustics in optics. The ray's source may be a point (called the radiant) or parallel rays from a point at infinity, in which case a direction vector of the rays must be specified.
More generally, especially as applied to symplectic geometry and singularity theory, a caustic is the critical value set of a Lagrangian mapping (π ○ i) : L ↪ M ↠ B; where i : L ↪ M is a Lagrangian immersion of a Lagrangian submanifold L into a symplectic manifold M, and π : M ↠ B is a Lagrangian fibration of the symplectic manifold M. The caustic is a subset of the Lagrangian fibration's base space B.
A catacaustic is the reflective case.
With a radiant, it is the evolute of the orthotomic of the radiant.
The planar, parallel-source-rays case: suppose the direction vector is ( a , b ) and the mirror curve is parametrised as ( u ( t ) , v ( t ) ) . The normal vector at a point is ( − v ′ ( t ) , u ′ ( t ) ) ; the reflection of the direction vector is (normal needs special normalization)
2 proj n d − d = 2 n n ⋅ n n ⋅ d n ⋅ n − d = 2 n n ⋅ d n ⋅ n − d = ( a v ′ 2 − 2 b u ′ v ′ − a u ′ 2 , b u ′ 2 − 2 a u ′ v ′ − b v ′ 2 ) v ′ 2 + u ′ 2 Having components of found reflected vector treat it as a tangent
( x − u ) ( b u ′ 2 − 2 a u ′ v ′ − b v ′ 2 ) = ( y − v ) ( a v ′ 2 − 2 b u ′ v ′ − a u ′ 2 ) . Using the simplest envelope form
F ( x , y , t ) = ( x − u ) ( b u ′ 2 − 2 a u ′ v ′ − b v ′ 2 ) − ( y − v ) ( a v ′ 2 − 2 b u ′ v ′ − a u ′ 2 ) = x ( b u ′ 2 − 2 a u ′ v ′ − b v ′ 2 ) − y ( a v ′ 2 − 2 b u ′ v ′ − a u ′ 2 ) + b ( u v ′ 2 − u u ′ 2 − 2 v u ′ v ′ ) + a ( − v u ′ 2 + v v ′ 2 + 2 u u ′ v ′ ) F t ( x , y , t ) = 2 x ( b u ′ u ″ − a ( u ′ v ″ + u ″ v ′ ) − b v ′ v ″ ) − 2 y ( a v ′ v ″ − b ( u ″ v ′ + u ′ v ″ ) − a u ′ u ″ ) + b ( u ′ v ′ 2 + 2 u v ′ v ″ − u ′ 3 − 2 u u ′ u ″ − 2 u ′ v ′ 2 − 2 u ″ v v ′ − 2 u ′ v v ″ ) + a ( − v ′ u ′ 2 − 2 v u ′ u ″ + v ′ 3 + 2 v v ′ v ″ + 2 v ′ u ′ 2 + 2 v ″ u u ′ + 2 v ′ u u ″ ) which may be unaesthetic, but F = F t = 0 gives a linear system in ( x , y ) and so it is elementary to obtain a parametrisation of the catacaustic. Cramer's rule would serve.
Let the direction vector be (0,1) and the mirror be ( t , t 2 ) . Then
u ′ = 1 u ″ = 0 v ′ = 2 t v ″ = 2 a = 0 b = 1 F ( x , y , t ) = ( x − t ) ( 1 − 4 t 2 ) + 4 t ( y − t 2 ) = x ( 1 − 4 t 2 ) + 4 t y − t F t ( x , y , t ) = − 8 t x + 4 y − 1 and F = F t = 0 has solution ( 0 , 1 / 4 ) ; i.e., light entering a parabolic mirror parallel to its axis is reflected through the focus.