Carnot's theorem (thermodynamics)

Proof

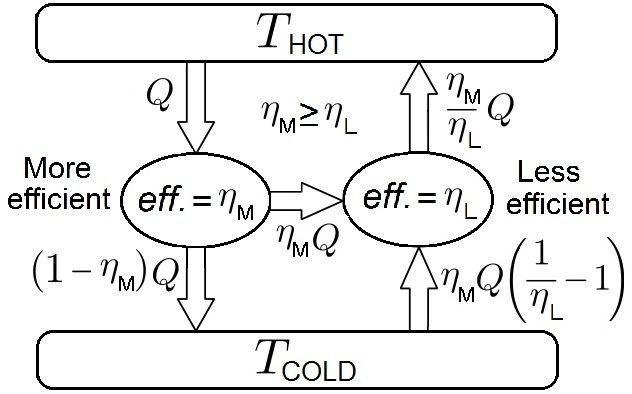
The proof of the Carnot theorem is a proof by contradiction, or reductio ad absurdum, as illustrated by the figure showing two heat engines operating between two reservoirs of different temperature. The heat engine with more efficiency ( η M ) is driving a heat engine with less efficiency ( η L ), causing the latter to act as a heat pump. This pair of engines receives no outside energy, and operates solely on the energy released when heat is transferred from the hot and into the cold reservoir. However, if η M > η L , then the net heat flow would be backwards, i.e., into the hot reservoir:

It is generally agreed that this is impossible because it violates the second law of thermodynamics.

We begin by verifying the values of work and heat flow depicted in the figure. First, we must point out an important caveat: the engine with less efficiency ( η L ) is being driven as a heat pump, and therefore must be a reversible engine. If the less efficient engine ( η L ) is not reversible, then the device could be built, but the expressions for work and heat flow shown in the figure would not be valid.

By restricting our discussion to cases where engine ( η L ) has less efficiency than engine ( η M ), we are able to simplify notation by adopting the convention that all symbols, Q and W represent non-negative quantities (since the direction of energy flow never changes sign in all cases where η L ⩽ η M ). Conservation of energy demands that for each engine, the energy which enters, E i n , must equal the energy which exits, E o u t :

The figure is also consistent with the definition of efficiency as η = W / Q h for both engines:

It may seem odd that a hypothetical heat pump with low efficiency is being used to violate the second law of thermodynamics, but the figure of merit for refrigerator units is not efficiency, W / Q h , but the coefficient of performance (COP), which is Q c / W . A reversible heat engine with low thermodynamic efficiency, W / Q h delivers more heat to the hot reservoir for a given amount of work when it is being driven as a heat pump.

Having established that the heat flow values shown in the figure are correct, Carnot's theorem may be proven for irreversible and the reversible heat engines.

Reversible engines

To see that every reversible engine operating between reservoirs T 1 and T 2 must have the same efficiency, assume that two reversible heat engines have different values of η , and let the more efficient engine (M) drive the less efficient engine (L) as a heat pump. As the figure shows, this will cause heat to flow from the cold to the hot reservoir without any external work or energy, which violates the second law of thermodynamics. Therefore both (reversible) heat engines have the same efficiency, and we conclude that:

This is an important result because it helps establish the Clausius theorem, which implies that the change in entropy is unique for all reversible processes.,

over all paths (from a to b in V-T space). If this integral were not path independent, then entropy, S, would lose its status as a state variable.

Irreversible engines

If one of the engines is irreversible, it must be the (M) engine, placed so that it reverse drives the less efficient but reversible (L) engine. But if this irreversible engine is more efficient than the reversible engine, (i.e., if η M > η L ), then the second law of thermodynamics is violated. And, since the Carnot cycle represents a reversible engine, we have the first part of Carnot's theorem:

Definition of thermodynamic temperature

The efficiency of the engine is the work divided by the heat introduced to the system or

where w_cy is the work done per cycle. Thus, the efficiency depends only on q_C/q_H.

Because all reversible engines operating between the same heat reservoirs are equally efficient, any reversible heat engine operating between temperatures T₁ and T₂ must have the same efficiency, meaning, the efficiency is the function of the temperatures only:

In addition, a reversible heat engine operating between temperatures T₁ and T₃ must have the same efficiency as one consisting of two cycles, one between T₁ and another (intermediate) temperature T₂, and the second between T₂andT₃. This can only be the case if

Specializing to the case that T 1 is a fixed reference temperature: the temperature of the triple point of water. Then for any T₂ and T₃,

Therefore, if thermodynamic temperature is defined by

then the function f, viewed as a function of thermodynamic temperature, is

and the reference temperature T₁ has the value 273.16. (Of course any reference temperature and any positive numerical value could be used—the choice here corresponds to the Kelvin scale.)

It follows immediately that

Substituting Equation 3 back into Equation 1 gives a relationship for the efficiency in terms of temperature:

Applicability to fuel cells and batteries

Since fuel cells and batteries can generate useful power when all components of the system are at the same temperature ( T = T H = T C ), they are clearly not limited by Carnot's theorem, which states that no power can be generated when T H = T C . This is because Carnot's theorem applies to engines converting thermal energy to work, whereas fuel cells and batteries instead convert chemical energy to work. Nevertheless, the second law of thermodynamics still provides restrictions on fuel cell and battery energy conversion.