Trisha Shetty (Editor)

Carathéodory's theorem (convex hull)

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Carathéodory's theorem (convex hull)

In convex geometry, Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d + 1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r ≤ d . The smallest r that makes the last statement valid for each x in the convex hull of P is defined as the Carathéodory's number of P. Depending on the properties of P, upper bounds lower than the one provided by Carathéodory's theorem can be obtained.

Contents

The similar theorems of Helly and Radon are closely related to Carathéodory's theorem: the latter theorem can be used to prove the former theorems and vice versa.

The result is named for Constantin Carathéodory, who proved the theorem in 1907 for the case when P is compact. In 1914 Ernst Steinitz expanded Carathéodory's theorem for any sets P in Rd.

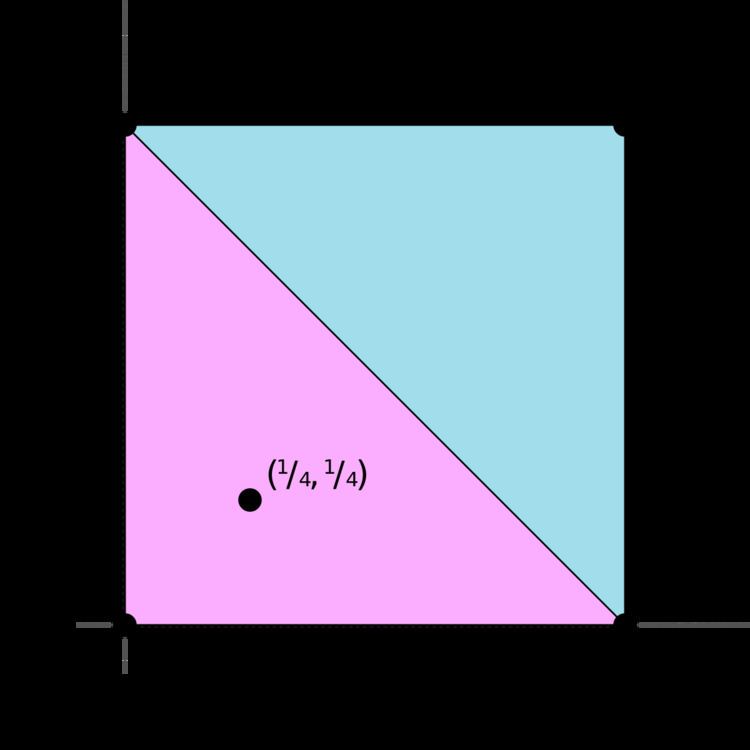
Example

Consider a set P = {(0,0), (0,1), (1,0), (1,1)} which is a subset of R2. The convex hull of this set is a square. Consider now a point x = (1/4, 1/4), which is in the convex hull of P. We can then construct a set {(0,0),(0,1),(1,0)} = P′, the convex hull of which is a triangle and encloses x, and thus the theorem works for this instance, since |P′| = 3. It may help to visualise Carathéodory's theorem in 2 dimensions, as saying that we can construct a triangle consisting of points from P that encloses any point in P.

Proof of Carathéodory's theorem

Let x be a point in the convex hull of P. Then, x is a convex combination of a finite number of points in P :

x = ∑ j = 1 k λ j x j

where every xj is in P, every λj is strictly positive, and ∑ j = 1 k λ j = 1 .

Suppose k > d + 1 (otherwise, there is nothing to prove). Then, the points x2 − x1, ..., xk − x1 are linearly dependent,

so there are real scalars μ2, ..., μk, not all zero, such that

∑ j = 2 k μ j ( x j − x 1 ) = 0 .

If μ1 is defined as

μ 1 := − ∑ j = 2 k μ j

then

∑ j = 1 k μ j x j = 0 ∑ j = 1 k μ j = 0

and not all of the μj are equal to zero. Therefore, at least one μj > 0. Then,

x = ∑ j = 1 k λ j x j − α ∑ j = 1 k μ j x j = ∑ j = 1 k ( λ j − α μ j ) x j

for any real α. In particular, the equality will hold if α is defined as

α := min 1 ≤ j ≤ k { λ j μ j : μ j > 0 } = λ i μ i .

Note that α > 0, and for every j between 1 and k,

λ j − α μ j ≥ 0.

In particular, λi − αμi = 0 by definition of α. Therefore,

x = ∑ j = 1 k ( λ j − α μ j ) x j

where every λ j − α μ j is nonnegative, their sum is one , and furthermore, λ i − α μ i = 0 . In other words, x is represented as a convex combination of at most k-1 points of P. This process can be repeated until x is represented as a convex combination of at most d + 1 points in P.

An alternative proof uses Helly's theorem.

References

Carathéodory's theorem (convex hull) Wikipedia
(Text) CC BY-SA


Similar Topics