Björling problem

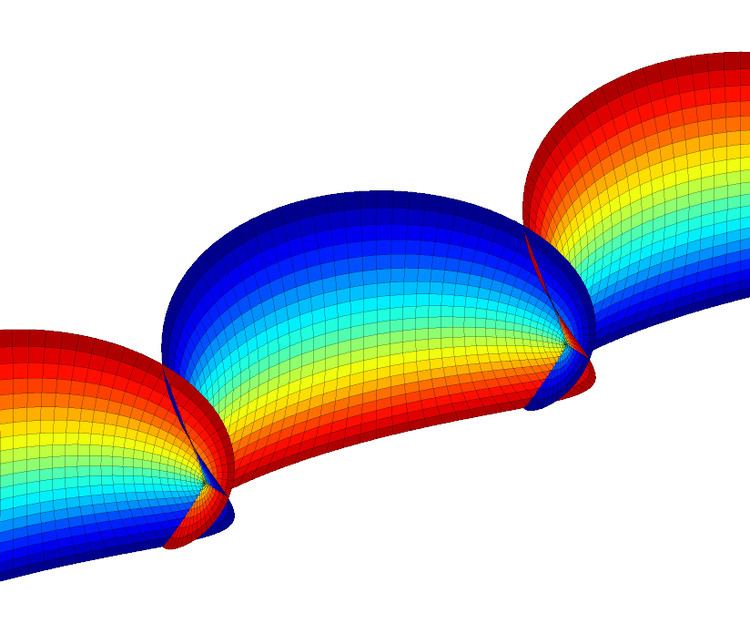
In differential geometry, the Björling problem is the problem of finding a minimal surface passing through a given curve with prescribed normal (or tangent planes). The problem was posed and solved by Swedish mathematician Emanuel Gabriel Björling, with further refinement by Hermann Schwarz.

The problem can be solved by extending the surface from the curve using complex analytic continuation. If c ( s ) is a real analytic curve in ℝ³ defined over an interval I, with c ′ ( s ) ≠ 0 and a vector field n ( s ) along c such that | | n ( t ) | | = 1 and c ′ ( t ) ⋅ n ( t ) = 0 , then the following surface is minimal:

where w = u + i v ∈ Ω , u 0 ∈ I , and I ⊂ Ω is a simply connected domain where the interval is included and the power series expansions of c ( s ) and n ( s ) are convergent.

A classic example is Catalan's minimal surface, which passes through a cycloid curve. Applying the method to a semicubical parabola produces the Henneberg surface, and to a circle (with a suitably twisted normal field) a minimal Möbius strip.

A unique solution always exists. It can be viewed as a Cauchy problem for minimal surfaces, allowing one to find a surface if a geodesic, asymptote or lines of curvature is known. In particular, if the curve is planar and geodesic, then the plane of the curve will be a symmetry plane of the surface.