Bertrand's ballot theorem

Example

Suppose there are 5 voters, of whom 3 vote for candidate A and 2 vote for candidate B (so p = 3 and q = 2). There are ten possibilities for the order of the votes cast:

AAABB

AABAB

ABAAB

BAAAB

AABBA

ABABA

BAABA

ABBAA

BABAA

BBAAA

For the order AABAB, the tally of the votes as the election progresses is:

For each column the tally for A is always larger than the tally for B so the A is always strictly ahead of B. For the order AABBA the tally of the votes as the election progresses is:

For this order, B is tied with A after the fourth vote, so A is not always strictly ahead of B. Of the 10 possible orders, A is always ahead of B only for AAABB and AABAB. So the probability that A will always be strictly ahead is

2 10 = 1 5 ,

and this is indeed equal to 3 − 2 3 + 2 as the theorem predicts.

Equivalent problems

Rather than computing the probability that a random vote counting order has the desired property, one can instead compute the number of favourable counting orders, then divide by the total number of ways in which the votes could have been counted. (This is the method used by Bertrand.) The total number of ways is the binomial coefficient ( p + q p ) ; Bertrand's proof shows that the number of favourable orders in which to count the votes is ( p + q − 1 p − 1 ) − ( p + q − 1 p ) (though he does not give this number explicitly). And indeed after division this gives p p + q − q p + q = p − q p + q .

Another equivalent problem is to calculate the number of random walks on the integers that consist of n steps of unit length, beginning at the origin and ending at the point m, that never become negative. Assuming n and m have the same parity and n ≥ m ≥ 0, this number is

( n n + m 2 ) − ( n n + m 2 + 1 ) = m + 1 n + m 2 + 1 ( n n + m 2 ) .

When m = 0 and n is even, this gives the Catalan number 1 n 2 + 1 ( n n 2 ) .

Proof by reflection

For A to be strictly ahead of B throughout the counting of the votes, there can be no ties. Separate the counting sequences according to the first vote. Any sequence that begins with a vote for B must reach a tie at some point, because A eventually wins. For any sequence that begins with A and reaches a tie, reflect the votes up to the point of the first tie (so any A becomes a B, and vice versa) to obtain a sequence that begins with B. Hence every sequence that begins with A and reaches a tie is in one-to-one correspondence with a sequence that begins with B, and the probability that a sequence begins with B is q / ( p + q ) , so the probability that A always leads the vote is

= 1 − the probability of sequences that tie at some point = 1 − the probability of sequences that tie at some point and begin with A or B = 1 − 2 q p + q = p − q p + q

Proof by induction

Another method of proof is by mathematical induction:

Clearly the theorem is true if p > 0 and q = 0 when the probability is 1, given that the first candidate receives all the votes; it is also true when p = q > 0 since the probability is 0, given that the first candidate will not be strictly ahead after all the votes have been counted.

Assume it is true both when p = a − 1 and q = b, and when p = a and q = b−1, with a > b > 0. Then considering the case with p = a and q = b, the last vote counted is either for the first candidate with probability a/(a + b), or for the second with probability b/(a + b). So the probability of the first being ahead throughout the count to the penultimate vote counted (and also after the final vote) is:

And so it is true for all p and q with p > q > 0.

Bertrand's and André's proofs

Bertrand expressed the solution as

2 m − μ μ

where μ = p + q is the total number of voters and m = p is the number of voters for the first candidate. He states that the result follows from the formula

P m + 1 , μ + 1 = P m , μ + P m + 1 , μ ,

where P m , μ is the number of favourable sequences, but "it seems probable that such a simple result could be shown in a more direct way". Indeed, a more direct proof was soon produced by Désiré André. His approach is often mistakenly labelled "the reflection principle" by modern authors but in fact uses a permutation. He shows that the "unfavourable" sequences (those that reach an intermediate tie) consist of an equal number of sequences that begin with A as those that begin with B. Every sequence that begins with B is unfavourable, and there are ( p + q − 1 q − 1 ) such sequences with a B followed by an arbitrary sequence of (q-1) B's and p A's. Each unfavourable sequence that begins with A can be transformed to an arbitrary sequence of (q-1) B's and p A's by finding the first B that violates the rule (by causing the vote counts to tie) and deleting it, and interchanging the order of the remaining parts. To reverse the process, take any sequence of (q-1) B's and p A's and search from the end to find where the number of A's first exceeds the number of B's, and then interchange the order of the parts and place a B in between. For example, the unfavourable sequence AABBABAA corresponds uniquely to the arbitrary sequence ABAAAAB. From this, it follows that the number of favourable sequences of p A's and q B's is

( p + q q ) − 2 ( p + q − 1 q − 1 ) = ( p + q q ) p − q p + q

and thus the required probability is

p − q p + q

as expected.

Variant: ties allowed

The original problem is to find the probability that the first candidate is always strictly ahead in the vote count. Consider now the problem to find the probability that the second candidate is never ahead (i.e. ties are allowed); the solution is

p + 1 − q p + 1 .

The variant problem can be solved by the reflection method in a similar way to the original problem. First note that the number of possible vote sequences is ( p + q q ) . Call a sequence "bad" if the second candidate is ever ahead, and if the number of bad sequences can be enumerated then the number of "good" sequences can be found by subtraction and the probability can be computed.

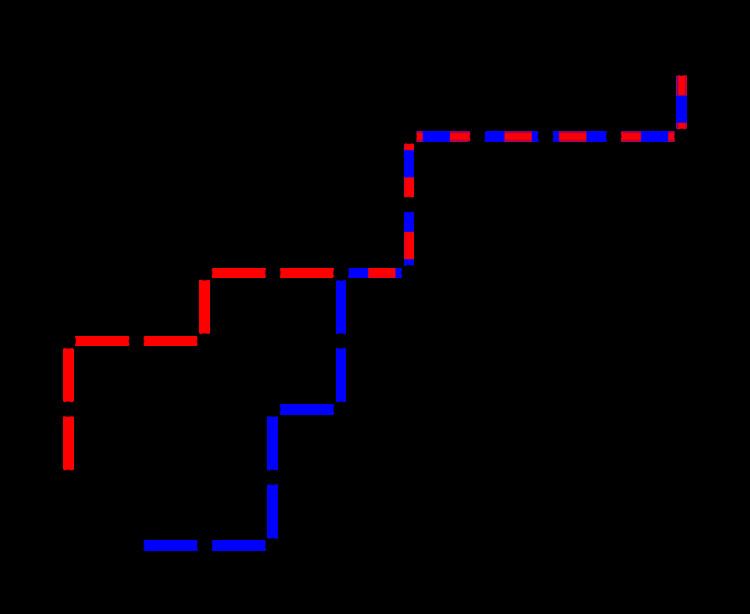
Represent a voting sequence as a lattice path on the Cartesian plane as follows:

Start the path at (0, 0)

Each time a vote for the first candidate is received move right 1 unit.

Each time a vote for the second candidate is received move up 1 unit.

Each such path corresponds to a unique sequence of votes and will end at (p, q). A sequence is 'good' exactly when the corresponding path never goes above the diagonal line y = x; equivalently, a sequence is 'bad' exactly when the corresponding path touches the line y = x + 1.

For each 'bad' path P, define a new path P′ by reflecting the part of P up to the first point it touches the line across it. P′ is a path from (−1, 1) to (p, q). The same operation applied again restores the original P. This produces a one-to-one correspondence between the 'bad' paths and the paths from (−1, 1) to (p, q). The number of these paths is ( p + q q − 1 ) and so that is the number of 'bad' sequences. This leaves the number of 'good' sequences as

( p + q q ) − ( p + q q − 1 ) = ( p + q q ) p + 1 − q p + 1 .

Since there are ( p + q q ) altogether, the probability of a sequence being good is p + 1 − q p + 1 .

In fact, the solutions to the original problem and the variant problem are easily related. For candidate A to be strictly ahead throughout the vote count, they must receive the first vote and for the remaining votes (ignoring the first) they must be either strictly ahead or tied throughout the count. Hence the solution to the original problem is

p p + q p − 1 + 1 − q p − 1 + 1 = p − q p + q

as required.

Conversely, the tie case can be derived from the non-tie case. Note that the number of non-tie sequences with p+1 votes for A is equal to the number of tie sequences with p votes for A. The number of non-tie votes with p + 1 votes for A votes is p + 1 − q p + 1 + q ( p + 1 + q q ) , which by algebraic manipulation is p + 1 − q p + 1 ( p + q q ) , so the fraction of sequences with p votes for A votes is p + 1 − q p + 1 .