The antisymmetric exchange is a contribution to the total magnetic exchange interaction between two neighboring magnetic spins,
S
i
and
S
j
. It was first postulated by Igor Dzyaloshinskii on the grounds of phenomenological considerations based on Landau theory. Toru Moriya identified the spin-orbit coupling as the microscopic mechanism of the antisymmetric exchange interaction. It can be written as
H
D
M
=
D
i
j
⋅
(
S
i
×
S
j
)
. This term is also called the Dzyaloshinskii-Moriya interaction. In magnetically ordered systems, it favors a spin canting of otherwise (anti)parallel aligned magnetic moments and thus, e.g., is a source of weak ferromagnetic behavior in an antiferromagnet.
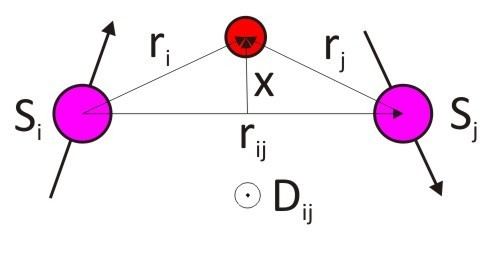
The orientation of the vector
D
i
j
is constrained by symmetry, as discussed already in Moriya’s original publication. Considering the case that the magnetic interaction between two neighboring ions is transferred via a single third ion (ligand) by the superexchange mechanism (see Figure), the orientation of
D
i
j
is obtained by the simple relation
D
i
j
∝
r
i
×
r
j
=
r
i
j
×
x
. This implies that
D
i
j
is oriented perpendicular to the triangle spanned by the involved three ions.
D
i
j
=
0
if the three ions are in line.
The antisymmetric exchange is of importance for the understanding of magnetism induced electric polarization in a recently discovered class of multiferroics: Here, small shifts of the ligand ions can be induced by magnetic ordering, because the systems tends to enhance the magnetic interaction energy on the cost of lattice energy. This mechanism is called “inverse Dzyaloshinskii-Moriya effect”. In certain magnetic structures, all ligand ions are shifted into the same direction, leading to a net electric polarization [4].