 | ||
Definitions
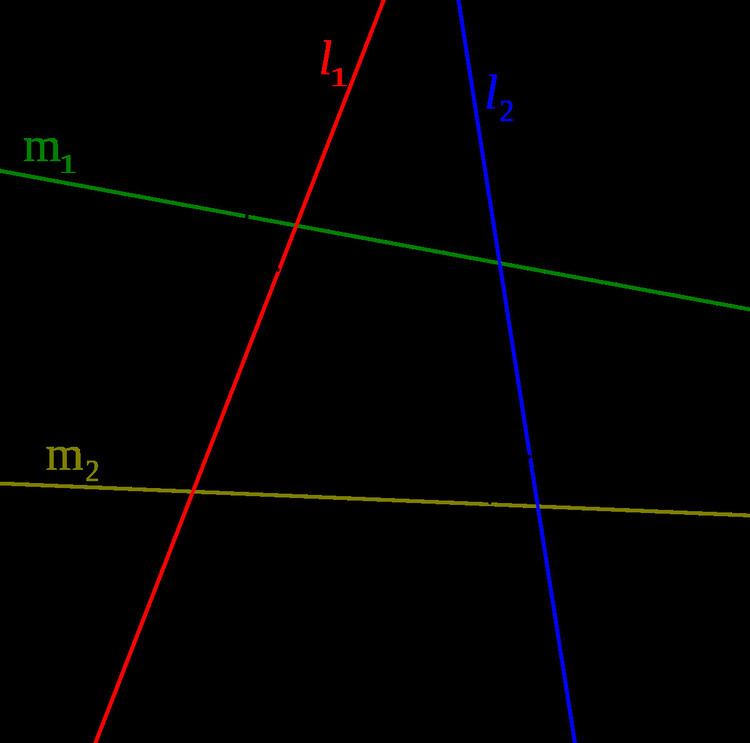
Given two lines
In any quadrilateral inscribed in a circle, any two opposite sides are anti-parallel with respect to the other two sides (Fig.2).
Two lines
Antiparallel vectors
In a Euclidean space, two directed line segments, often called vectors in applied mathematics, are antiparallel, if they are supported by parallel lines and have opposite directions. In that case, one of the associated Euclidean vectors is the product of the other by a negative number.
Relations
- The line joining the feet to two altitudes of a triangle is antiparallel to the third side.(any cevians which 'see' the third side with the same angle create antiparallel lines)
- The tangent to a triangle's circumcircle at a vertex is antiparallel to the opposite side.
- The radius of the circumcircle at a vertex is perpendicular to all lines antiparallel to the opposite sides.
