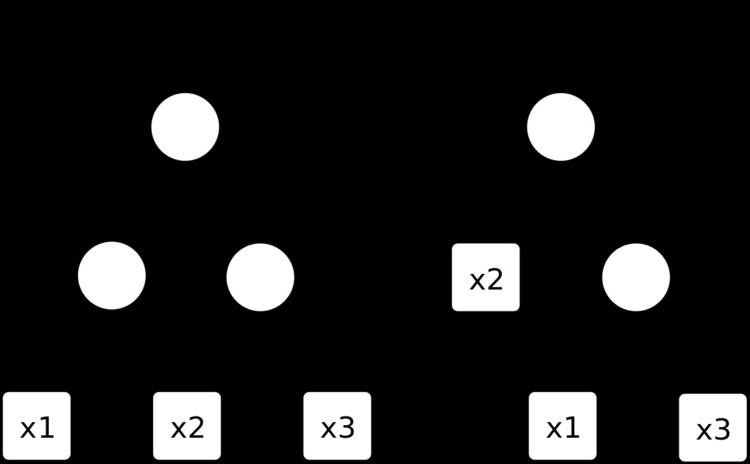
 | ||
An and-inverter graph (AIG) is a directed, acyclic graph that represents a structural implementation of the logical functionality of a circuit or network. An AIG consists of two-input nodes representing logical conjunction, terminal nodes labeled with variable names, and edges optionally containing markers indicating logical negation. This representation of a logic function is rarely structurally efficient for large circuits, but is an efficient representation for manipulation of boolean functions. Typically, the abstract graph is represented as a data structure in software.
Conversion from the network of logic gates to AIGs is fast and scalable. It only requires that every gate be expressed in terms of AND gates and inverters. This conversion does not lead to unpredictable increase in memory use and runtime. This makes the AIG an efficient representation in comparison with either the binary decision diagram (BDD) or the "sum-of-product" (ΣoΠ) form, that is, the canonical form in Boolean algebra known as the disjunctive normal form (DNF). The BDD and DNF may also be viewed as circuits, but they involve formal constraints that deprive them of scalability. For example, ΣoΠs are circuits with at most two levels while BDDs are canonical, that is, they require that input variables be evaluated in the same order on all paths.
Circuits composed of simple gates, including AIGs, are an "ancient" research topic. The interest in AIGs started in the late 1950s and continued in the 1970s when various local transformations have been developed. These transformations were implemented in several logic synthesis and verification systems, such as Darringer et al. and Smith et al., which reduce circuits to improve area and delay during synthesis, or to speed up formal equivalence checking. Several important techniques were discovered early at IBM, such as combining and reusing multi-input logic expressions and subexpressions, now known as structural hashing.
Recently there has been a renewed interest in AIGs as a functional representation for a variety of tasks in synthesis and verification. That is because representations popular in the 1990s (such as BDDs) have reached their limits of scalability in many of their applications. Another important development was the recent emergence of much more efficient boolean satisfiability (SAT) solvers. When coupled with AIGs as the circuit representation, they lead to remarkable speedups in solving a wide variety of boolean problems.
AIGs found successful use in diverse EDA applications. A well-tuned combination of AIGs and boolean satisfiability made an impact on formal verification, including both model checking and equivalence checking. Another recent work shows that efficient circuit compression techniques can be developed using AIGs. There is a growing understanding that logic and physical synthesis problems can be solved using simulation and boolean satisfiability to compute functional properties (such as symmetries) and node flexibilities (such as don't-care terms, resubstitutions, and SPFDs). Mishchenko et al. shows that AIGs are a promising unifying representation, which can bridge logic synthesis, technology mapping, physical synthesis, and formal verification. This is, to a large extent, due to the simple and uniform structure of AIGs, which allow rewriting, simulation, mapping, placement, and verification to share the same data structure.
In addition to combinational logic, AIGs have also been applied to sequential logic and sequential transformations. Specifically, the method of structural hashing was extended to work for AIGs with memory elements (such as D-type flip-flops with an initial state, which, in general, can be unknown) resulting in a data structure that is specifically tailored for applications related to retiming.
Ongoing research includes implementing a modern logic synthesis system completely based on AIGs. The prototype called ABC features an AIG package, several AIG-based synthesis and equivalence-checking techniques, as well as an experimental implementation of sequential synthesis. One such technique combines technology mapping and retiming in a single optimization step. These optimizations can be implemented using networks composed of arbitrary gates, but the use of AIGs makes them more scalable and easier to implement.
