Name Abu al-Quhi Died 1000 AD, Baghdad, Iraq | Role Mathematician | |
 | ||
Ab sahl al q h
Abū Sahl Wayjan ibn Rustam al-Qūhī (al-Kūhī; Persian: ابوسهل بیژن کوهی Abusahl Bijan-e Koohi) was a Persian mathematician, physicist and astronomer. He was from Kuh (or Quh), an area in Tabaristan, Amol, and flourished in Baghdad in the 10th century. He is considered one of the greatest Muslim geometers, with many mathematical and astronomical writings ascribed to him.

Al-Qūhī was the leader of the astronomers working in 988 AD at the observatory built by the Buwayhid amir Sharaf al-Dawla in Badhdad. He wrote a treatise on the astrolabe in which he solves a number of difficult geometric problems.
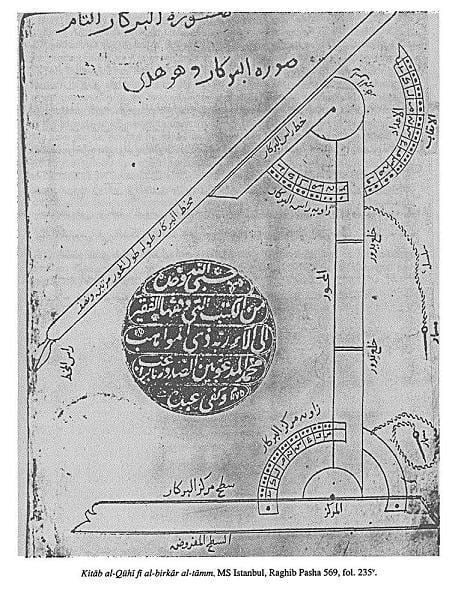
In mathematics he devoted his attention to those Archimedean and Apollonian problems leading to equations higher than the second degree. He solved some of them and discussed the conditions of solvability. For example, he was able to solve the problem of inscribing an equilateral pentagon into a square, resulting in an equation of fourth degree. He also wrote a treatise on the "perfect compass", a compass with one leg of variable length that allows to draw any conic section: straight lines, circles, ellipses, parabolas and hyperbolas. It is likely that al-Qūhī invented the device.
Like Aristotle, al-Qūhī proposed that the weight of bodies varies with their distance from the center of the Earth.
The correspondence between al-Qūhī and Abu Ishaq al-Sabi, a high civil servant interested in mathematics, has been preserved.
