(ε, δ) definition of limit

History

Although the Greeks examined limiting process, such as the Babylonian method, they probably had no concept similar to the modern limit. The need for the concept of a limit came into force in the 17th century when Pierre de Fermat attempted to find the slope of the tangent line at a point x of a function such as f ( x ) = x 2 . Using a non-zero, but almost zero quantity, E , Fermat performed the following calculation:

s l o p e = f ( x + E ) − f ( x ) E = ( x + E ) 2 − x 2 E = x 2 + 2 x E + E 2 − x 2 E = 2 x E + E 2 E = 2 x + E = 2 x .

The key to the above calculation is that since E is non-zero one can divide f ( x + E ) − f ( x ) by E , but since E is close to 0, 2 x + E is essentially 2 x . Quantities such as E are called infinitesimals. The problem with this calculation is that mathematicians of the era were unable to rigorously define a quantity with properties of E .

This problem reappeared later in the 1600s at the center of the development of calculus because calculations such as Fermat's are important to the calculation of derivatives. Isaac Newton first developed calculus via an infinitesimal quantity called a fluxion. He developed them in reference to the idea of an "infinitely small moment in time..." However, Netwon later rejected fluxions in favor of a theory of ratios that is close to the modern ϵ − δ definition of the limit. Moreover, Isaac Newton was aware that the limit of the ratio of vanishing quantities was not itself a ratio, as he wrote:

Those ultimate ratios ... are not actually ratios of ultimate quantities, but limits ... which they can approach so closely that their difference is less than any given quantity...

Additionally, Newton occasionally explained limits in terms similar to the epsilon–delta definition. Gottfried Wilhelm Leibniz developed an infinitesimal of his own and tried to provide it with a rigorous footing, but it was still greeted with unease by some mathematicians and philosophers.

Augustin-Louis Cauchy gave a definition of limit in terms of a more primitive notion he called a variable quantity. He never gave an epsilon–delta definition of limit (Grabiner 1981). Some of Cauchy's proofs contain indications of the epsilon–delta method. Whether or not his foundational approach can be considered a harbinger of Weierstrass's is a subject of scholarly dispute. Grabiner feels that it is, while Schubring (2005) disagrees. Nakane concludes that Cauchy and Weierstrass gave the same name to different notions of limit.

Eventually, Weierstrass and Bolzano are credited with providing a rigorous footing for calculus in the form of the modern ϵ − δ definition of the limit. The need for reference to an infinitesimal E was then removed and Fermat's computation turned into the computation of the following limit:

lim h → 0 f ( x + h ) − f ( x ) h .

This is not to say that the limiting definition was free of problems as although it removed the need to use infinitesimals, it did require the construction of the real numbers by Richard Dedekind. This is also not to say that infinitesimals have no place in modern mathematics as later mathematicians were able to rigorously create infinitesimal quantities as part of the hyperreal number or surreal number systems. Moreover, it is possible to rigorously develop calculus with these quantities and they have other mathematical uses.

Informal statement

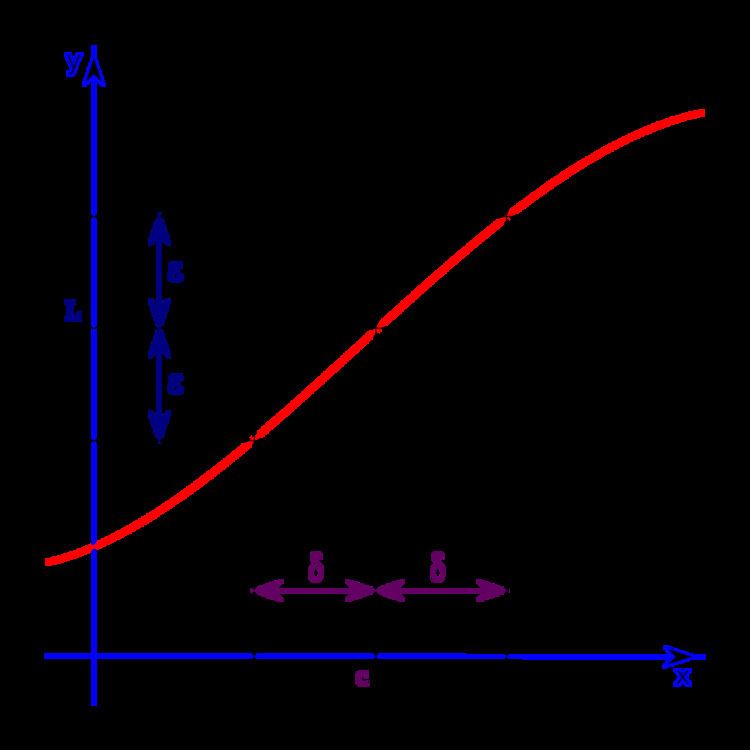
A viable intuitive or provisional definition is that a "function f approaches the limit L near a (symbolically, lim x → a f ( x ) = L ) if we can make f(x) as close as we like to L by requiring that x be sufficiently close to, but unequal to, a."

When we say that two things are close (such as f(x) and L or x and a) we mean that the distance between them is small. When f(x), L, x, and a are real numbers, distance is the absolute value of one quantity minus the other. Thus, when we say f(x) is close to L we mean | f ( x ) − L | is small. When we say that x and a are close, we mean that | x − a | is small.

When we say that we can make f(x) as close as we like to L, we mean that for all non-zero distances, ϵ , we can make the distance between f(x) and L smaller than ϵ .

When we say that we can make f(x) as close as we like to L by requiring that x be sufficiently close to, but, unequal to, a, we mean that for all non-zero distances ϵ , there is some non-zero distance δ such that if the distance between x and a is less than δ then the distance between f(x) and L is smaller than ϵ .

The aspect that must be grasped is that the definition requires the following conversation. One is provided with any challenge ϵ > 0 for a given f,a, and L. One must answer with a δ > 0 such that 0 < | x − a | < δ implies that | f ( x ) − L | < ϵ . If one can provide an answer for any challenge, one has proven that the limit exists.

Precise statement for real valued functions

The ( ε , δ ) definition of the limit of a function is as follows:

Let f be a real valued function defined on a subset D of the real numbers. Let c be a limit point of D and let L be a real number. We say that

lim x → c f ( x ) = L

if for every ϵ > 0 there exists a δ such that, for all x ∈ D , if 0 < | x − c | < δ , then | f ( x ) − L | < ϵ .

Symbolically:

lim x → c f ( x ) = L ⟺ ( ∀ ε > 0 ) ( ∃   δ > 0 ) ( ∀ x ∈ D ) ( 0 < | x − c | < δ   ⇒   | f ( x ) − L | < ε )

If D = [ a , b ] or D = ( a , b ) or D = R , then the condition that c is a limit point is automatically met because closed real intervals and the entire real line are perfect sets.

Precise statement for functions between metric spaces

The definition can be generalized to functions that map between metric spaces. These spaces come with a function, called a metric, that takes two points in the space and returns a real number that represents the distance between the two points. The generalized definition is as follows:

Suppose f is defined on a subset D of a metric space X with a metric d X ( x , y ) and maps into a metric space Y with a metric d Y ( x , y ) . Let c be a limit point of D and let L be a point of Y .

We say that

lim x → c f ( x ) = L

if for every ϵ > 0 there exists a δ such that, for all x ∈ D , if 0 < d X ( x , c ) < δ , then d Y ( f ( x ) , L ) < ϵ .

Since d ( x , y ) = | x − y | is a metric on the real numbers, one can show that this definition generalizes the first definition for real functions.

Negation of the precise statement

The negation of the definition is a follows:

Suppose f is defined on a subset D of a metric space X with a metric d X ( x , y ) and maps into a metric space Y with a metric d Y ( x , y ) . Let c be a limit point of D and let L be a point of Y .

We say that

lim x → c f ( x ) ≠ L

if there exists an ϵ > 0 such that for all δ > 0 there is an x ∈ D such that 0 < d X ( x , c ) < δ and d Y ( f ( x ) , L ) > ϵ .

We say that lim x → c f ( x ) does not exist if for all L ∈ Y , lim x → c f ( x ) ≠ L .

For the negation of a real valued function defined on the real numbers, simply set d Y ( x , y ) = d X ( x , y ) = | x − y | .

Precise statement for limits at infinity

The precise statement for limits at infinity is as follows:

Suppose f is defined on a subset D of a metric space X with a metric d X ( x , y ) and maps into a metric space Y with a metric d Y ( x , y ) . Let L ∈ Y .

We say that

lim x → ∞ f ( x ) = L

if for every ϵ > 0 , there is a real number N > 0 such that there is an x ∈ D where d X ( x , 0 ) > N and such that if d X ( x , 0 ) > N and x ∈ D , then d Y ( f ( x ) , L ) < ϵ .

Example 1

We will show that

lim x → 0 x sin ⁡ ( 1 x ) = 0

We let ϵ > 0 be given. We need to find a δ > 0 such that | x − 0 | < δ implies | x sin ⁡ ( 1 x ) − 0 | < ϵ .

Since sine is bounded above by 1 and below by -1,

| x sin ⁡ ( 1 x ) − 0 | = | x sin ⁡ ( 1 x ) | = | x | | sin ⁡ ( 1 x ) | ≤ | x | .

Thus, if we take δ = ϵ , then | x | = | x − 0 | < δ implies | x sin ⁡ ( 1 x ) − 0 | ≤ | x | < ϵ , which completes the proof.

Example 2

Let us prove the statement that

lim x → a x 2 = a 2

for any real number a .

Let ϵ > 0 be given. We will find a δ > 0 such that | x − a | < δ implies | x 2 − a 2 | < ϵ .

We start by factoring:

| x 2 − a 2 | = | x − a | | x + a | .

We recognize that | x − a | is the term bounded by δ so we can presuppose a bound of 1 and later pick something smaller than that for δ .

So we suppose | x − a | < 1 . Since | x | − | y | ≤ | x − y | holds in general for real numbers x and y , we have

| x | − | a | ≤ | x − a | < 1.

Thus,

| x | < 1 + | a | .

Thus via the triangle inequality,

| x + a | ≤ | x | + | a | < 2 | a | + 1.

Thus, if we further suppose that

| x − a | < ϵ 2 | a | + 1

then

| x 2 − a 2 | < ϵ .

In summary, we set

δ = min ( 1 , ϵ 2 | a | + 1 ) .

So, if | x − a | < δ , then

| x 2 − a 2 | = | x − a | | x + a | ≤ ϵ 2 | a | + 1 ( | x + a | ) ≤ ϵ 2 | a | + 1 ( 2 | a | + 1 ) ≤ ϵ

Thus, we have found a δ such that | x − a | < δ implies | x 2 − a 2 | < ϵ . Thus, we have shown that

lim x → a x 2 = a 2

for any real number a .

Example 3

Let us prove the statement that

lim x → 5 ( 3 x − 3 ) = 12.

This is easily shown through graphical understandings of the limit, and as such serves as a strong basis for introduction to proof. According to the formal definition above, a limit statement is correct if and only if confining x to δ units of c will inevitably confine f ( x ) to ε units of L . In this specific case, this means that the statement is true if and only if confining x to δ units of 5 will inevitably confine

3 x − 3

to ε units of 12. The overall key to showing this implication is to demonstrate how δ and ε must be related to each other such that the implication holds. Mathematically, we want to show that

0 < | x − 5 | < δ   ⇒   | ( 3 x − 3 ) − 12 | < ε .

Simplifying, factoring, and dividing 3 on the right hand side of the implication yields

| x − 5 | < ε / 3 ,

which immediately gives the required result if we choose

δ = ε / 3.

Thus the proof is completed. The key to the proof lies in the ability of one to choose boundaries in x , and then conclude corresponding boundaries in f ( x ) , which in this case were related by a factor of 3, which is entirely due to the slope of 3 in the line

y = 3 x − 3.

Continuity

A function f is said to be continuous at c if it is both defined at c and its value at c equals the limit of f as x approaches c:

lim x → c f ( x ) = f ( c ) .

If the condition 0 < |x − c| is left out of the definition of limit, then requiring f(x) to have a limit at c would be the same as requiring f(x) to be continuous at c.

f is said to be continuous on an interval I if it is continuous at every point c of I.

Comparison with infinitesimal definition

Keisler proved that a hyperreal definition of limit reduces the quantifier complexity by two quantifiers. Namely, f ( x ) converges to a limit L as x tends to a if and only if for every infinitesimal e, the value f ( x + e ) is infinitely close to L; see microcontinuity for a related definition of continuity, essentially due to Cauchy. Infinitesimal calculus textbooks based on Robinson's approach provide definitions of continuity, derivative, and integral at standard points in terms of infinitesimals. Once notions such as continuity have been thoroughly explained via the approach using microcontinuity, the epsilon–delta approach is presented as well. Karel Hrbáček argues that the definitions of continuity, derivative, and integration in Robinson-style non-standard analysis must be grounded in the ε–δ method in order to cover also non-standard values of the input. Błaszczyk et al. argue that microcontinuity is useful in developing a transparent definition of uniform continuity, and characterize the criticism by Hrbáček as a "dubious lament". Hrbáček proposes an alternative non-standard analysis, which (unlike Robinson's) has many "levels" of infinitesimals, so that limits at one level can be defined in terms of infinitesimals at the next level.